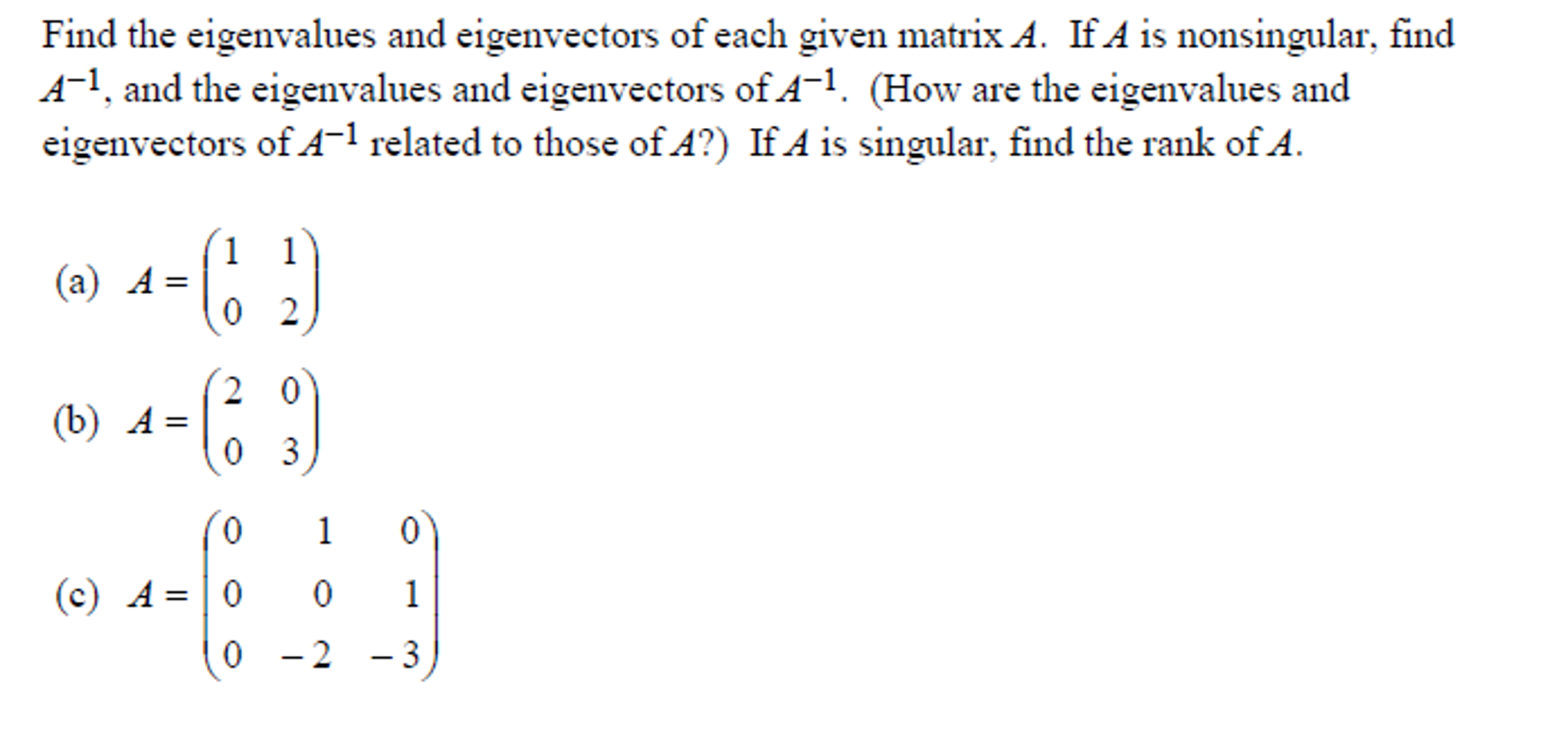Understanding how to find eigenvalues and eigenvectors is crucial for anyone studying linear algebra or its applications in fields like physics, engineering, and computer science. Eigenvalues and eigenvectors play a vital role in solving systems of linear equations, analyzing transformations, and working with matrices. This article will guide you step-by-step through the process of finding eigenvalues and eigenvectors, ensuring you have a solid foundation in this fundamental concept.
Eigenvalues and eigenvectors are essential tools in mathematics and its practical applications. Whether you're working with data science, machine learning algorithms, or solving differential equations, these concepts are indispensable. By mastering the techniques outlined in this article, you'll be able to confidently tackle problems involving matrices and their transformations.
This guide is designed for students, researchers, and professionals who want to deepen their understanding of eigenvalues and eigenvectors. We'll cover the theory behind these concepts, step-by-step methods for finding them, and practical examples to reinforce your learning. Let's dive in and explore this fascinating area of mathematics.
Read also:Chris Kyle Confirmed Kills The Untold Story Of The Most Lethal Sniper In Us History
Table of Contents
- Introduction to Eigenvalues and Eigenvectors
- Definitions and Key Concepts
- How to Find Eigenvalues and Eigenvectors
- Practical Examples
- Properties of Eigenvalues and Eigenvectors
- Applications in Real Life
- Common Mistakes to Avoid
- Using Software Tools for Computation
- Frequently Asked Questions
- Conclusion and Call to Action
Introduction to Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors are mathematical constructs that describe how a matrix transforms vectors in space. They provide insight into the behavior of linear transformations and are widely used in various scientific disciplines. Understanding how to find eigenvalues and eigenvectors is crucial for anyone working with matrices, as they reveal important properties of the system being analyzed.
At their core, eigenvalues represent scaling factors, while eigenvectors represent specific directions in space that remain unchanged under a given transformation. Together, they form the backbone of many advanced mathematical techniques, including principal component analysis (PCA), Google's PageRank algorithm, and quantum mechanics.
In this section, we'll explore why eigenvalues and eigenvectors are important and how they relate to real-world problems. By the end of this article, you'll have a clear understanding of the significance of these concepts and how to apply them effectively.
Definitions and Key Concepts
Before diving into the process of finding eigenvalues and eigenvectors, let's define some key terms:
- Eigenvalue: A scalar value λ that satisfies the equation Av = λv, where A is a square matrix, v is a non-zero vector, and λ is the eigenvalue.
- Eigenvector: A non-zero vector v that satisfies the equation Av = λv, where A is a square matrix and λ is the corresponding eigenvalue.
- Characteristic Polynomial: A polynomial derived from the determinant of the matrix (A - λI), where I is the identity matrix.
These definitions form the foundation for understanding the process of finding eigenvalues and eigenvectors. By grasping these concepts, you'll be better equipped to solve problems involving linear transformations.
How to Find Eigenvalues and Eigenvectors
The process of finding eigenvalues and eigenvectors involves several steps. Below, we'll break down the procedure into manageable parts:
Read also:Nashville Television Show Cast The Ultimate Guide To The Stars
Step 1: Form the Characteristic Equation
The first step in finding eigenvalues is to form the characteristic equation. This involves calculating the determinant of the matrix (A - λI), where A is the given matrix, λ is the eigenvalue, and I is the identity matrix. The resulting equation is a polynomial in λ, known as the characteristic polynomial.
For example, consider the matrix:
A = [[2, 1], [1, 2]]
To form the characteristic equation, subtract λ from the diagonal elements and calculate the determinant:
det(A - λI) = det([[2-λ, 1], [1, 2-λ]])
Simplify the determinant to obtain the characteristic polynomial:
(2-λ)(2-λ) - 1 = λ² - 4λ + 3
Step 2: Solve for Eigenvalues
Once you have the characteristic polynomial, solve for the eigenvalues by finding the roots of the equation. This can be done using factoring, the quadratic formula, or numerical methods for higher-degree polynomials.
Continuing with the example above:
λ² - 4λ + 3 = 0
Factor the equation:
(λ - 3)(λ - 1) = 0
The eigenvalues are λ₁ = 3 and λ₂ = 1.
Step 3: Find Eigenvectors
After finding the eigenvalues, the next step is to determine the corresponding eigenvectors. For each eigenvalue, solve the equation (A - λI)v = 0, where v is the eigenvector.
Using λ₁ = 3:
(A - 3I)v = 0
Substitute the values:
[[2-3, 1], [1, 2-3]]v = [[-1, 1], [1, -1]]v = 0
Solve the system of equations to find the eigenvector:
v₁ = [1, 1]
Similarly, for λ₂ = 1:
(A - 1I)v = 0
Substitute the values:
[[2-1, 1], [1, 2-1]]v = [[1, 1], [1, 1]]v = 0
Solve the system of equations to find the eigenvector:
v₂ = [-1, 1]
Practical Examples
Let's explore a few practical examples to solidify your understanding:
- Example 1: Find the eigenvalues and eigenvectors of the matrix A = [[4, 1], [2, 3]].
- Example 2: Solve for the eigenvalues and eigenvectors of a 3x3 matrix.
- Example 3: Use eigenvalues and eigenvectors to analyze the stability of a system.
Each example will walk you through the process step-by-step, ensuring you gain hands-on experience with these concepts.
Properties of Eigenvalues and Eigenvectors
Eigenvalues and eigenvectors have several important properties:
- Eigenvalues can be real or complex numbers, depending on the matrix.
- The sum of the eigenvalues equals the trace of the matrix (the sum of the diagonal elements).
- The product of the eigenvalues equals the determinant of the matrix.
- Eigenvectors corresponding to distinct eigenvalues are linearly independent.
Understanding these properties will deepen your comprehension of how eigenvalues and eigenvectors interact within a system.
Applications in Real Life
Eigenvalues and eigenvectors have numerous applications in real-world scenarios:
- Principal Component Analysis (PCA): Reducing the dimensionality of data while preserving variance.
- Google's PageRank Algorithm: Ranking web pages based on their importance.
- Quantum Mechanics: Describing the states of particles in quantum systems.
By mastering these concepts, you'll be able to apply them to a wide range of fields and solve complex problems.
Common Mistakes to Avoid
When working with eigenvalues and eigenvectors, it's easy to make mistakes. Here are some common pitfalls to avoid:
- Forgetting to subtract λ from the diagonal elements when forming the characteristic equation.
- Making arithmetic errors when solving for eigenvalues or eigenvectors.
- Assuming that all eigenvalues are real without verifying the matrix's properties.
Double-check your work and practice regularly to minimize errors.
Using Software Tools for Computation
For larger matrices or more complex problems, using software tools can save time and effort. Popular tools for computing eigenvalues and eigenvectors include:
- Python (using libraries like NumPy and SciPy)
- Matlab
- Mathematica
These tools provide efficient algorithms for solving eigenvalue problems and can handle matrices of any size.
Frequently Asked Questions
Here are some common questions about eigenvalues and eigenvectors:
- What happens if a matrix has no eigenvalues?
- Can eigenvalues be zero?
- How do eigenvalues relate to matrix diagonalization?
Each question will be answered in detail, providing clarity on these important topics.
Conclusion and Call to Action
In conclusion, understanding how to find eigenvalues and eigenvectors is a fundamental skill for anyone working with linear algebra and its applications. By following the steps outlined in this article and practicing with practical examples, you'll gain confidence in solving eigenvalue problems.
We encourage you to leave a comment below sharing your thoughts or asking questions. Additionally, feel free to explore other articles on our site for more in-depth coverage of related topics. Together, let's continue learning and expanding our knowledge in mathematics and beyond!